Doku Überblick
ALLES LEBT
Doku zum Wirbelweltbild -
Fraktale 03b
Gerechnet mit Qt TwinFractals Version1.4 und 1.5
Beispiele für Orbits im Vierpol
Das Bild 03-27 in Bilder 03 ist das Startbild der Serie ohne Orbit. Unter dem Bild 03-27 steht ein Kommentar, der zuerst gelesen werden sollte.
03b-1
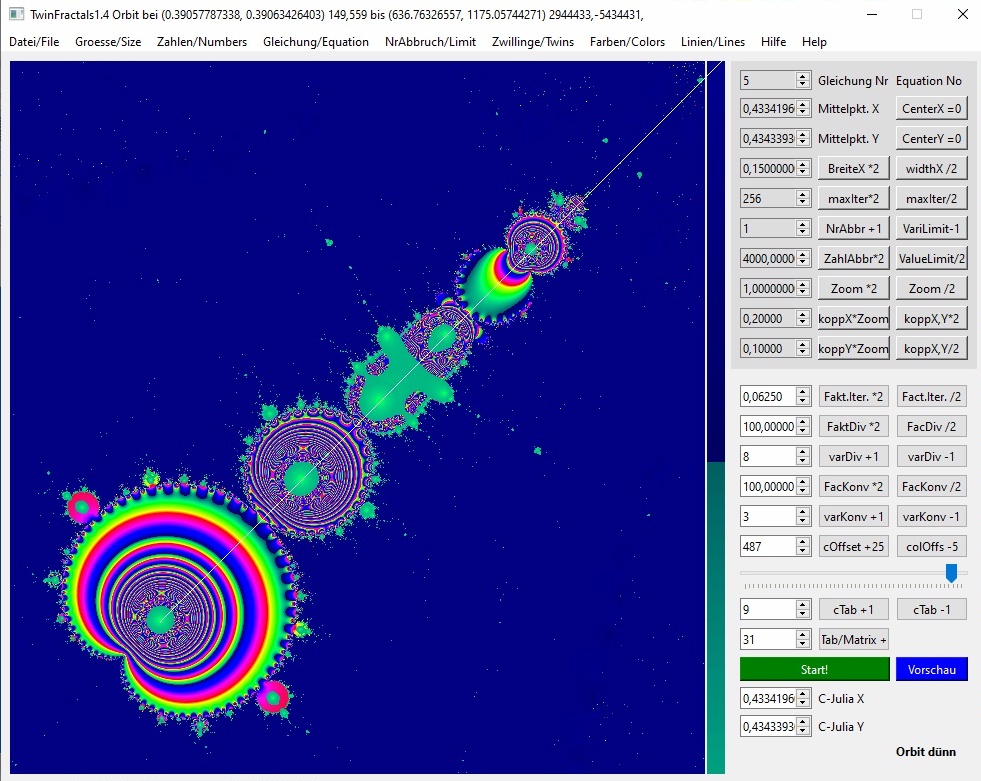
Die vierte Iteration muss größer als 4000 gewesen sein. Es kam zum Abbruch schon nach 3 Iterationen (Orbit-Liste):
1. (0.3907937007194206, 0.3902026093525295) 150,560
2. (0.8620056375703175, 0.8601675648184243) 2330,-1614
3. (363.0093093865954756, -67.1909389948051086) 1677865,313246
03b-2
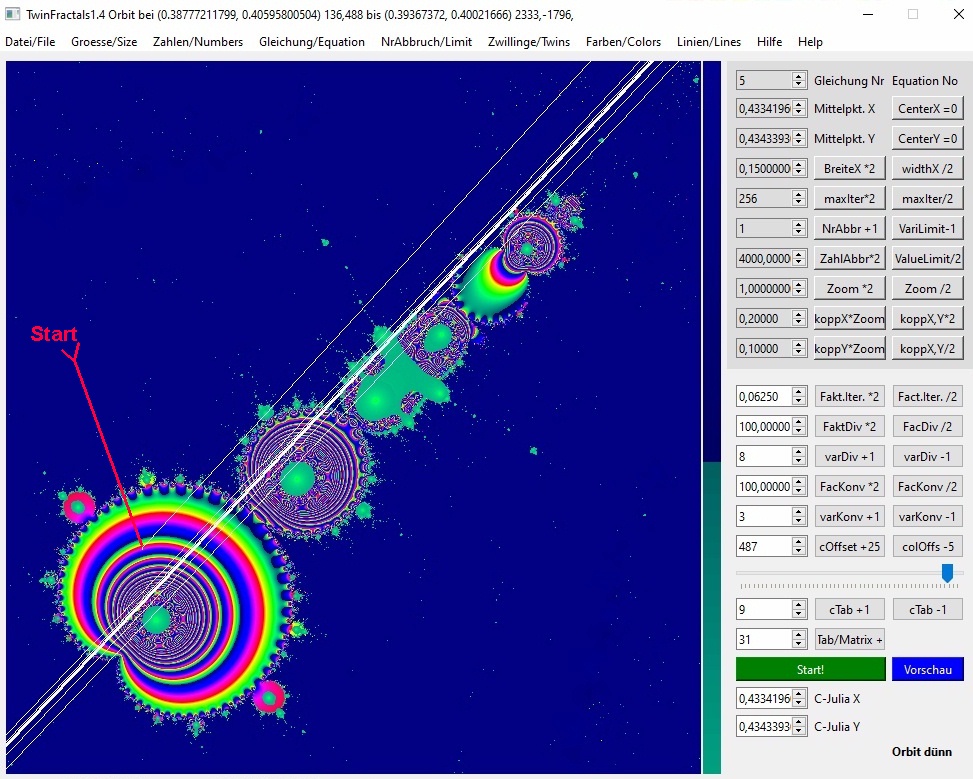
Der Start ist hier etwas nördlicher im Bauch. Es ergeben sich Vierer-Zyklen mit jeweils 14 gleichen Ziffern nach dem Komma (allein bis zur 250.Iteration), die vermutlich zu keinem späteren Divergieren mehr führen, wie man auch an der konsistenten Farbe in 03-24 erkennen kann. Daraus ist zu schlussfolgern, dass auch der Startpunkt von Bild 1 kein divergentes Verhalten hat, sondern bei sehr großen Zahlen (ca. 5000 Iterationen folgen dort noch) auch zum Zyklus einschwenken wird. Die Orbit-Liste ist derzeit noch nicht so lang.
Orbit-Liste am Schluss:
243. (-14.5160800813334987, 0.4837724801956929) -68819,127
244. (0.0059017356217380, -0.0057414604004475) -1631,2391
245. (0.3936737205320588, 0.4002166597029915) 163,514
246. (0.8627902169390419, 0.8994947646883477) 2333,-1796
247. (-14.5160800813348576, 0.4837724801974393) -68819,127
248. (0.0059017356217382, -0.0057414604004451) -1631,2391
249. (0.3936737205320591, 0.4002166597029939) 163,514
250. (0.8627902169390420, 0.8994947646883521) 2333,-1796
03b-3
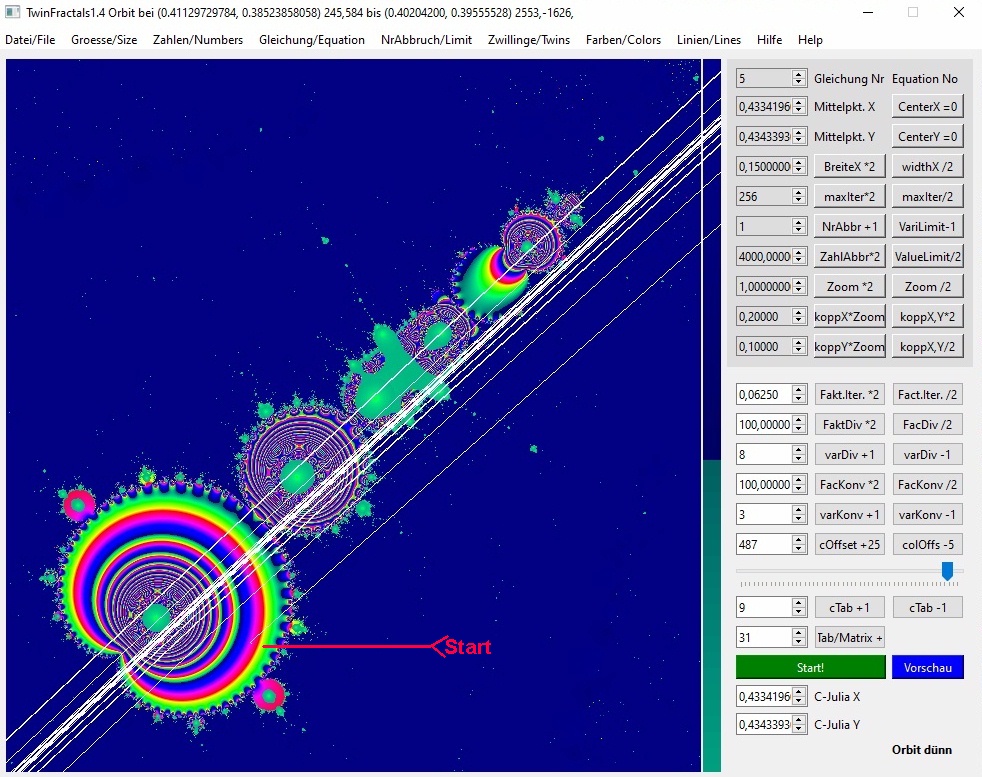
Hier der Start noch weiter außen, aber auf der anderen Seite. Es endet wieder klar im Viererzyklus.
243. (0.7124170232869428, -11.1189463147405849) 1638,53810
244. (-0.0092557856914880, 0.0103174678652242) -1700,2318
245. (0.4020419773977307, 0.3955553414062304) 202,535
246. (0.9101913327913335, 0.8626143834726016) 2553,-1626
247. (0.7124071311108295, -11.1189703729590672) 1638,53810
248. (-0.0092557668703410, 0.0103174068865331) -1700,2318
249. (0.4020419962170335, 0.3955552804390883) 202,535
250. (0.9101913636003784, 0.8626142687931572) 2553,-1626
03b-4
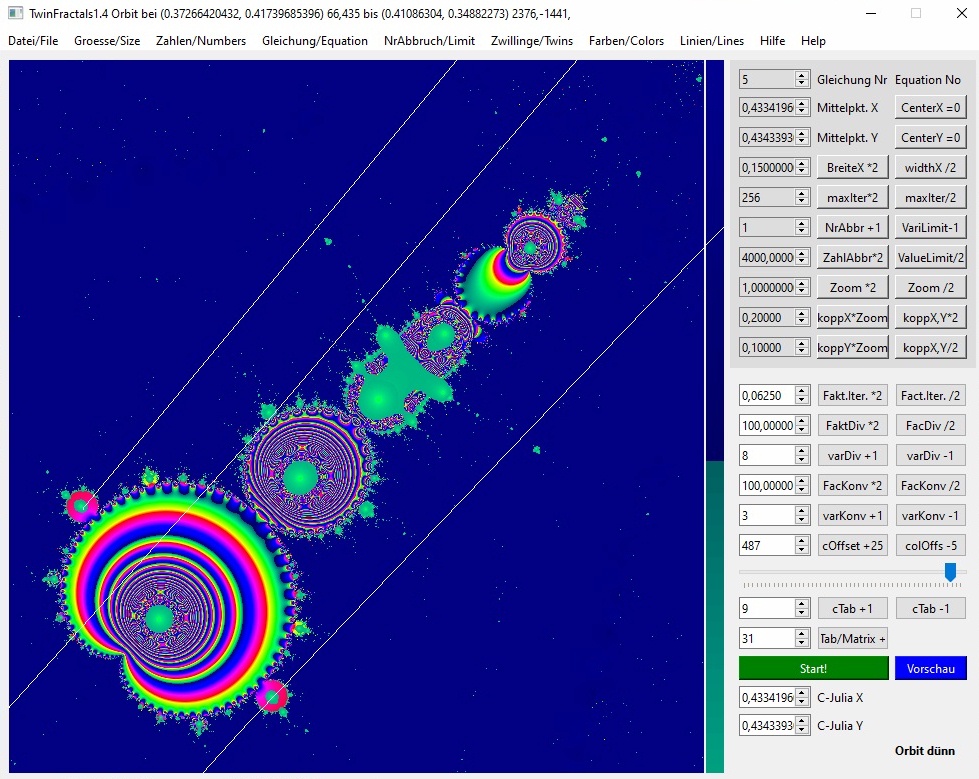
Start mittig im linken "Arm". Abbruch nach 11 Iterationen:
1. (0.3743908230215808, 0.4143752712230303) 74,448
2. (0.8074426496112384, 0.9334935681725445) 2077,-1954
3. (-5.0408475430003481, 4.0280091258205282) -24980,-16271
4. (0.0390978859317558, 0.0180197456787398) -1478,2282
5. (0.4135148246666890, 0.4323896625000618) 255,365
6. (0.8785815432837283, 0.9748831179182553) 2406,-2145
7. (-5.3481311759906713, -0.0249719973847674) -26402,2480
8. (0.0348493506040718, -0.0474225949971493) -1497,2584
9. (0.4092200899814367, 0.3670119342334315) 235,667
10. (0.8729133255519181, 0.8507250733354497) 2380,-1571
11. (-107.1285823997334319, 3.4196986257283468) -497306,-13457
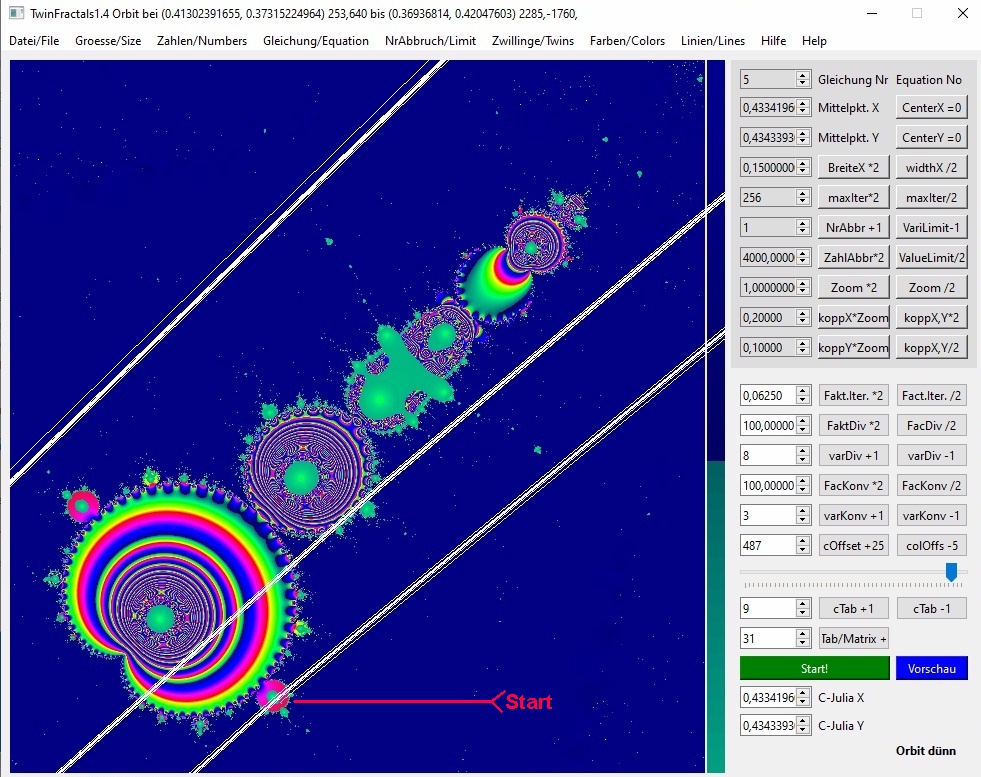
03b-5
Start auf der rechtesten dünnen Linie nach oben, nicht mehr im Zentrum des (diesmal rechten) "Armes". Diesmal wird es ein Zwölfer-Zyklus:
1. (0.4169088086330865, 0.3725047676259129) 270,642
2. (0.9408671762742554, 0.8007930223598224) 2695,-1340
3. (3.6819426152025407, -4.4996698491364864) 15377,23184
4. (0.0227318436142853, 0.0479910162192376) -1553,2143
5. (0.4396322694608513, 0.4205460224255636) 376,420
6. (0.9945046141083785, 0.8887733064230176) 2943,-1747
7. (-0.2399927947131839, -4.5421972675804989) -2768,23380
8. (-0.0698493221998528, 0.0392806427415107) -1981,2184
...
227. (-1.5509077899692369, 42.0453528372755869) -8833,-192171
228. (-0.0007003138788419, 0.0007402384838615) -1661,2362
229. (0.4162084949387206, 0.3732450058352749) 267,639
230. (0.9397712265982353, 0.8022735154664639) 2690,-1346
231. (3.7126641362544159, -4.5825961331666978) 15519,23567
232. (0.0216676489421656, 0.0468058933338018) -1558,2149
233. (0.4385675948897262, 0.4193563583096533) 371,425
234. (0.9920829678883317, 0.8865068190139125) 2932,-1736
235. (-0.1825318570776719, -4.6280257027261387) -2502,23778
236. (-0.0664456671626006, 0.0399224833731953) -1965,2181
237. (0.3506040510512333, 0.4124233554815220) -36,457
238. (0.8250387831944416, 0.8747060841111945) 2159,-1682
239. (-1.5226922130886895, 42.0637312878641438) -8702,-192256
240. (-0.0007007609904223, 0.0007386637076389) -1661,2362
241. (0.4162080478278194, 0.3732434310604929) 267,639
242. (0.9397700854750773, 0.8022707845413968) 2690,-1346
243. (3.7127550756424776, -4.5824842759263724) 15519,23567
244. (0.0216701427649471, 0.0468054098733890) -1558,2149
245. (0.4385700950886334, 0.4193558778801282) 371,425
246. (0.9920880420288921, 0.8865053696089416) 2932,-1736
247. (-0.1824626025621303, -4.6278735448377999) -2502,23777
248. (-0.0664492632861586, 0.0399266029555314) -1965,2181
249. (0.3506004833093269, 0.4124274665159993) -36,457
250. (0.8250321080000764, 0.8747127944140527) 2159,-1682
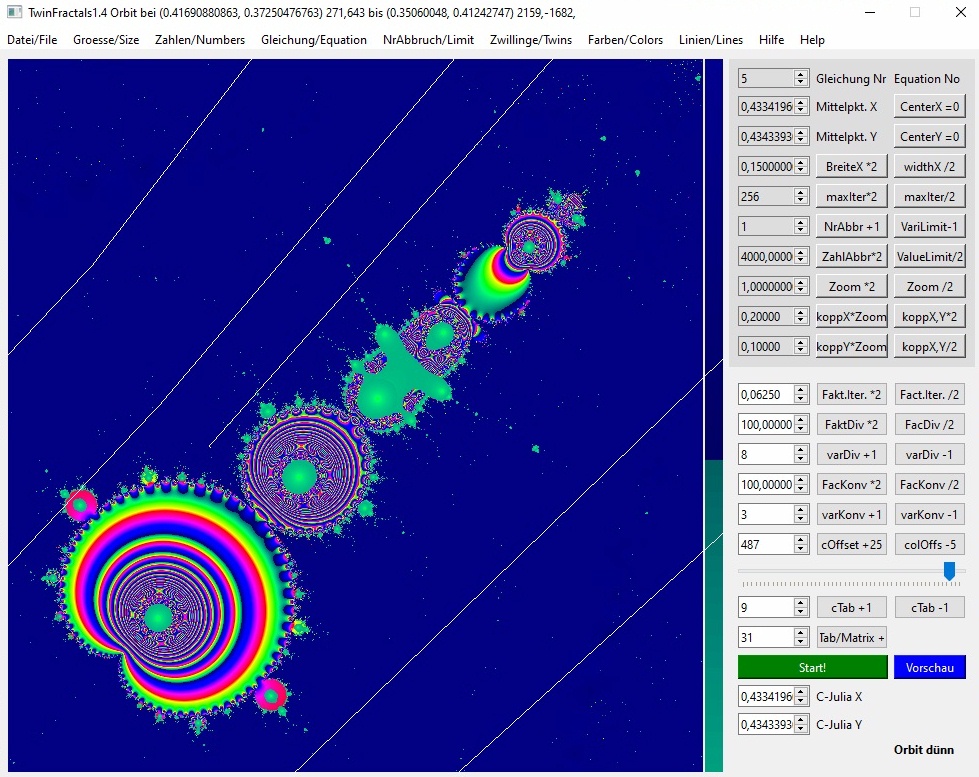
03b-6
Das ist außerhalb des Apfelmännchens. Wie zu erwarten, geht es immer näher zum Fixpunkt (0, 1). Nach Iteration 83 bricht hier lediglich der Orbit-Algorithmus ab, weil Änderungen schon lange nicht mehr darstellbar sind.
1. (0.4020167223021531, 0.4275407388489280) 201,387
2. (0.8950792980678758, 0.9839414729729830) 2483,-2187
3. (-4.3076893038204114, -1.0816521005054316) -21588,7369
4. (0.0125073069920448, -0.0760078442113657) -1601,2716
5. (0.4146560957753472, 0.3515947335258009) 260,739
6. (0.9181478545977310, 0.8377876599827960) 2589,-1511
7. (-0.2636582217837196, -10.7617014807637386) -2877,52157
8. (-0.0105455883180449, 0.0094047702670806) -1706,2322
9. (0.3914719728019299, 0.4369450193931101) 153,344
10. (0.8718199009996644, 1.0008745964768491) 2375,-2265
11. (-4.1111903773562188, -0.3076518603301054) -20679,3788
12. (0.0419412066875624, -0.0811519897737674) -1464,2740
13. (0.4440157564704280, 0.3466340195371149) 396,762
14. (0.9706193385994493, 0.8218852983707596) 2832,-1437
15. (0.8014072992886239, -5.8161468423983020) 2049,29275
16. (-0.0251466452499775, 0.0395414650538917) -1774,2183
17. (0.3768795941580645, 0.4670472344482940) 85,205
18. (0.8320713541526726, 1.0567043861076606) 2191,-2524
19. (-3.0431123488750096, 0.4681705034367687) -15737,199
...
74. (0.0000236164116242, 1.0000069123016209) -1658,-2261
75. (-0.0000145921572559, 1.0000144748822444) -1658,-2261
76. (-0.0000046889552315, 0.9999834857691023) -1658,-2261
77. (0.0000139673805085, 1.0000032411314292) -1658,-2261
78. (-0.0000080107950003, 1.0000089028327073) -1658,-2261
79. (-0.0000032734712669, 0.9999905477003805) -1658,-2261
80. (0.0000082326876861, 1.0000014241235813) -1658,-2261
81. (-0.0000043661747356, 1.0000054438889516) -1658,-2261
82. (-0.0000022166574339, 0.9999946092395942) -1658,-2261
83. (0.0000048364599054, 1.0000005565104668) -1658,-2261
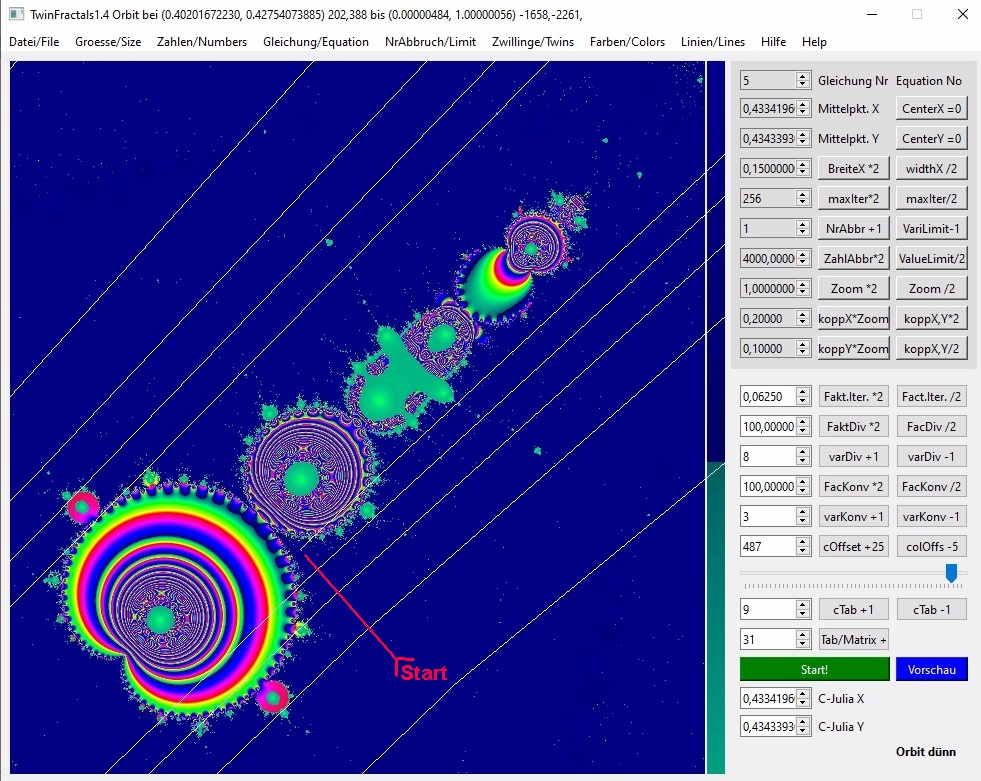
03b-7
Hier das Gleiche, mit Start "im Hals" (roter Pfeil) außerhalb des Apfelmännchens. Wieder zu (0,1) am Schluss, was ich nicht erwartet hätte, weil es auf der anderen Seite (von Bild 6) nach meiner Vermutung anders sein sollte:
1. (0.4212253553956760, 0.4057421776978514) 290,488
2. (0.9627363257288156, 0.9091304122055307) 2796,-1841
3. (-2.0890966723190392, -4.5970173204798712) -11323,23634
4. (-0.0588855597980332, -0.0086423995767285) -1930,2404
5. (0.3623101130623172, 0.3971590450097783) 18,528
6. (0.8506718593011821, 0.8926014917567097) 2277,-1764
7. (-15.8271353953219158, -3.9188884006764431) -74884,20497
8. (0.0018405087206891, -0.0059549522343563) -1650,2392
9. (0.4230659183796088, 0.3997872875170281) 299,516
10. (0.9657868204286852, 0.8969113293086508) 2810,-1784
11. (-1.6684310918641712, -4.8533365755513307) -9377,24820
12. (-0.0582240522050867, 0.0020063940205208) -1927,2356
13. (0.3630053411167186, 0.4078115816120158) 21,479
14. (0.8507957256638444, 0.9118368763288541) 2278,-1853
15. (-11.1417893164763377, -1.8640265315428668) -53207,10989
16. (0.0054780221932212, -0.0116092517335725) -1633,2418
17. (0.4267035944213666, 0.3941336110983134) 316,542
18. (0.9722496018462640, 0.8850744912384054) 2840,-1730
19. (-1.1463580780128988, -4.9066282761137652) -6961,25067
20. (-0.0594587467443543, 0.0135788170705227) -1933,2303
21. (0.3618092332736992, 0.4193808618419451) 15,425
22. (0.8468918313003491, 0.9328275998488913) 2260,-1951
23. (-8.4523243642173362, -0.5976974988577786) -40764,5130
24. (0.0130260982138437, -0.0184839063873357) -1598,2450
...
105. (-0.0000022632293770, 1.0000391421659189) -1658,-2262
106. (-0.0000297430771703, 0.9999830026744243) -1658,-2261
...
116. (0.0000036259537342, 0.9999918904912364) -1658,-2261
117. (0.0000049344794791, 1.0000059911972983) -1658,-2261
118. (-0.0000066068396358, 1.0000015302504273) -1658,-2261
119. (0.0000013725996359, 0.9999942357373444) -1658,-2261
120. (0.0000039760150725, 1.0000033159843162) -1658,-2261
121. (-0.0000041409504123, 1.0000018209637778) -1658,-2261
122. (0.0000001860066982, 0.9999960519046477) -1658,-2261
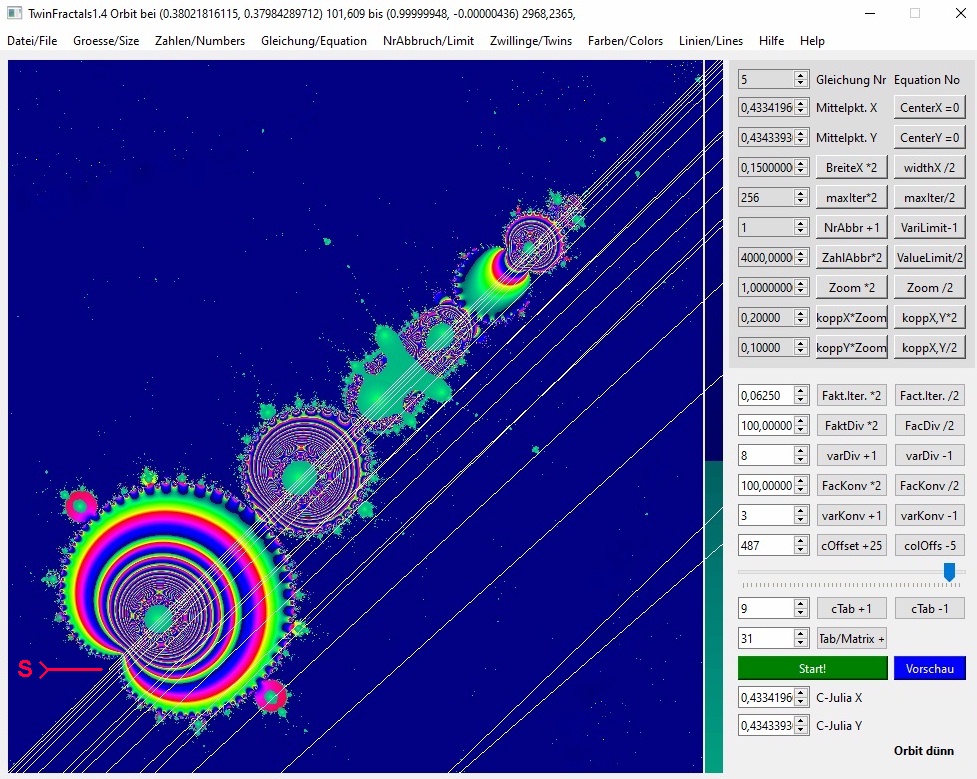
03b-8
Hier liegt der Start unten links (roter Pfeil), die linkeste Linie. Ergebnis: Der Fixpunkt (1,0) wird angepeilt. Ab Iteration 79 spielt sich alles im gleichen Pixel ab.
1. (0.3802181611510765, 0.3798428971223149) 101,608
2. (0.8298052842033771, 0.8286882903909095) 2181,-1469
3. (9.2316370828201251, 8.9233407892353149) 41053,-38921
4. (-0.0080247754764545, -0.0086099047045831) -1695,2404
5. (0.3721930954192038, 0.3712326347310312) 64,648
6. (0.8164298169369437, 0.8143775253148698) 2119,-1402
7. (6.9370644259398322, 6.6514298716159876) 30437,-28410
8. (-0.0143988324216627, -0.0157172030901972) -1724,2437
9. (0.3658176879725939, 0.3641235666524828) 34,681
10. (0.8060448678154253, 0.8028530420058890) 2071,-1349
11. (5.8204522696155658, 5.5259900324589415) 25271,-23202
12. (-0.0206527106382110, -0.0230252649521592) -1753,2471
13. (0.3595607243251984, 0.3568111081329836) 5,715
14. (0.7960486782711873, 0.7912576013993630) 2025,-1296
15. (5.0418926448565520, 4.7251906943911459) 21669,-19497
16. (-0.0277604951293032, -0.0318295632095904) -1786,2512
17. (0.3524465468030589, 0.3479966444792585) -28,755
18. (0.7849043876939786, 0.7776078889552432) 1973,-1232
19. (4.3882430831379429, 4.0384485674801818) 18644,-16320
20. (-0.0369476457816288, -0.0440943531657527) -1828,2569
...
78. (1.0000767236944397, 0.0000581636764562) 2969,2365
79. (1.0000196441961471, -0.0000746882001514) 2968,2365
80. (0.9999386215027498, 0.0000082876815912) 2968,2365
81. (1.0000249196103521, 0.0000429737784522) 2968,2365
82. (1.0000242379412938, -0.0000316263393306) 2968,2365
83. (0.9999691371194517, -0.0000082928273235) 2968,2365
84. (1.0000032928870612, 0.0000254191642460) 2968,2365
85. (1.0000178393634527, -0.0000102187635263) 2968,2365
86. (0.9999869656000709, -0.0000100995040955) 2968,2365
87. (0.9999964997596215, 0.0000127535834677) 2968,2365
88. (1.0000105268033685, -0.0000013067629641) 2968,2365
89. (0.9999958103713299, -0.0000074048733649) 2968,2365
90. (0.9999957917382317, 0.0000053716909975) 2968,2365
91. (1.0000052701995275, 0.0000014766565045) 2968,2365
92. (0.9999994823723179, -0.0000043592012977) 2968,2365
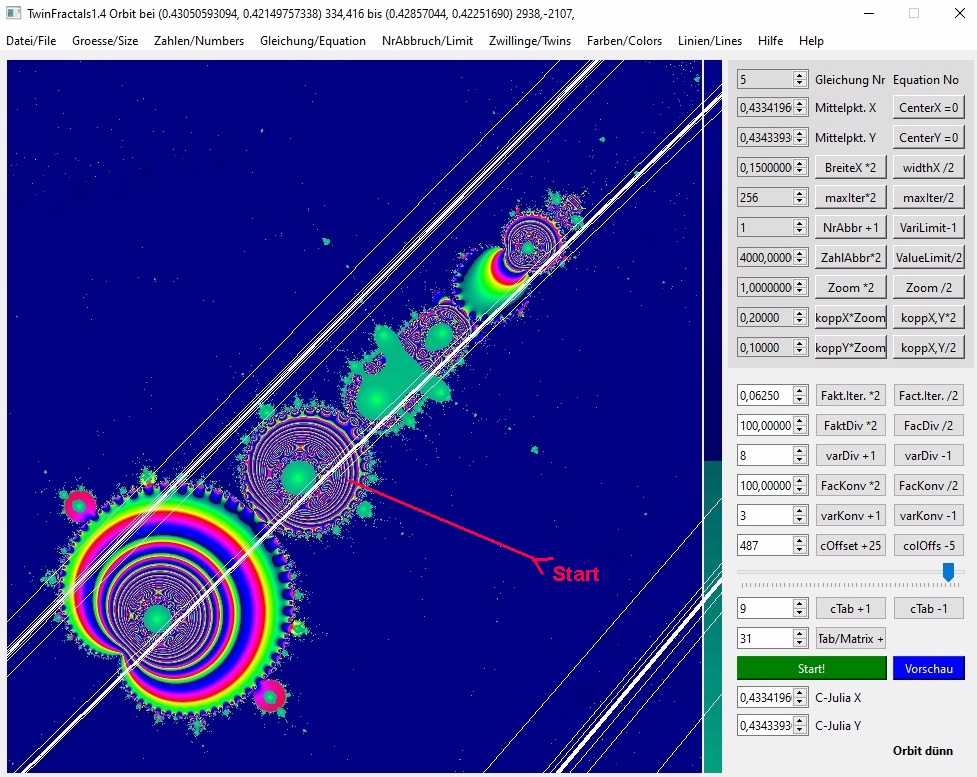
03b-9
Startpunkt roter Pfeil. Es entsteht ein Achter-Zyklus.
1. (0.4305059309352432, 0.4214975733813028) 333,415
2. (0.9977340253625907, 0.9643979471449332) 2958,-2097
3. (-1.9297818616740858, -2.5988910012368729) -10586,14389
4. (-0.1050610423307697, -0.0655465394281772) -2144,2668
5. (0.3248988042752141, 0.3558754683643691) -155,719
6. (0.8019295588623988, 0.8403642836578059) 2052,-1523
7. (-0.0469967704051347, 21.9501252308061012) -1875,-99194
8. (-0.0024500104128091, 0.0025150708707512) -1669,2354
9. (0.4280559310100347, 0.4240126325511657) 322,404
10. (0.9924799678669759, 0.9700593604037994) 2933,-2123
11. (-2.0375804863556324, -2.5272584853645630) -11085,14058
12. (-0.0997452534282474, -0.0716681990207598) -2119,2696
13. (0.3302504005781483, 0.3496623658250879) -131,748
14. (0.8107771314143575, 0.8307684463415290) 2093,-1478
15. (10.4365669776027481, 26.0550561585281422) 46628,-118187
16. (-0.0021479114718365, 0.0000459893846376) -1667,2365
17. (0.4283580197604194, 0.4215435663442261) 323,415
18. (0.9930249973984612, 0.9646269149832473) 2936,-2098
...
235. (-2.0081227915287130, -2.5781330573615544) -10948,14293
236. (-0.1007518098734578, -0.0681762216584665) -2124,2680
237. (0.3292451970054305, 0.3531976652561100) -135,731
238. (0.8090160947585326, 0.8363568561309510) 2085,-1504
239. (4.1927182481421061, 27.4658476084879482) 17740,-124714
240. (-0.0019354934493538, 0.0010193258742635) -1666,2361
241. (0.4285704412628139, 0.4225168996303050) 324,411
242. (0.9935416343649455, 0.9667491328653349) 2938,-2107
243. (-2.0081226245273367, -2.5781333072175361) -10948,14293
244. (-0.1007518157774681, -0.0681762041560644) -2124,2680
245. (0.3292451911036300, 0.3531976829773930) -135,731
246. (0.8090160844327796, 0.8363568841202841) 2085,-1504
247. (4.1926860119289069, 27.4658457720395504) 17740,-124714
248. (-0.0019354920189191, 0.0010193307986561) -1666,2361
249. (0.4285704426932565, 0.4225169045546722) 324,411
250. (0.9935416377543229, 0.9667491436003598) 2938,-2107
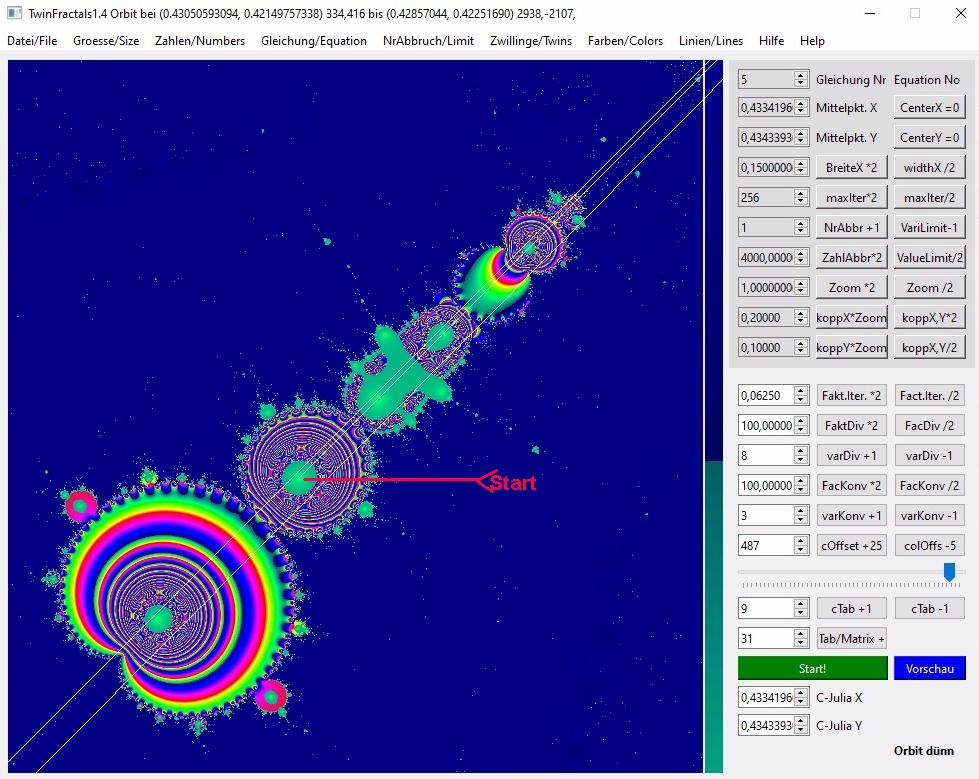
03b-10
Wieder scheinbar divergent (aber vermutlich nicht, nur sehr große Sprünge am Anfang), ein Kugel-Zentrum. Abbruch schon nach der siebenten Iteration.
1. (0.4212253553956760, 0.4208500913669144) 290,418
2. (0.9638209658134369, 0.9624688428031390) 2801,-2088
3. (-2.7231978315446361, -2.7614953825143749) -14257,15141
4. (-0.0657088219111758, -0.0642019894270841) -1962,2662
5. (0.3553467902850082, 0.3564894100971538) -14,716
6. (0.8400826526456003, 0.8415169000317370) 2228,-1528
7. (-716.0119475931496709, 238.8789476434214123) -3314406,-1102888
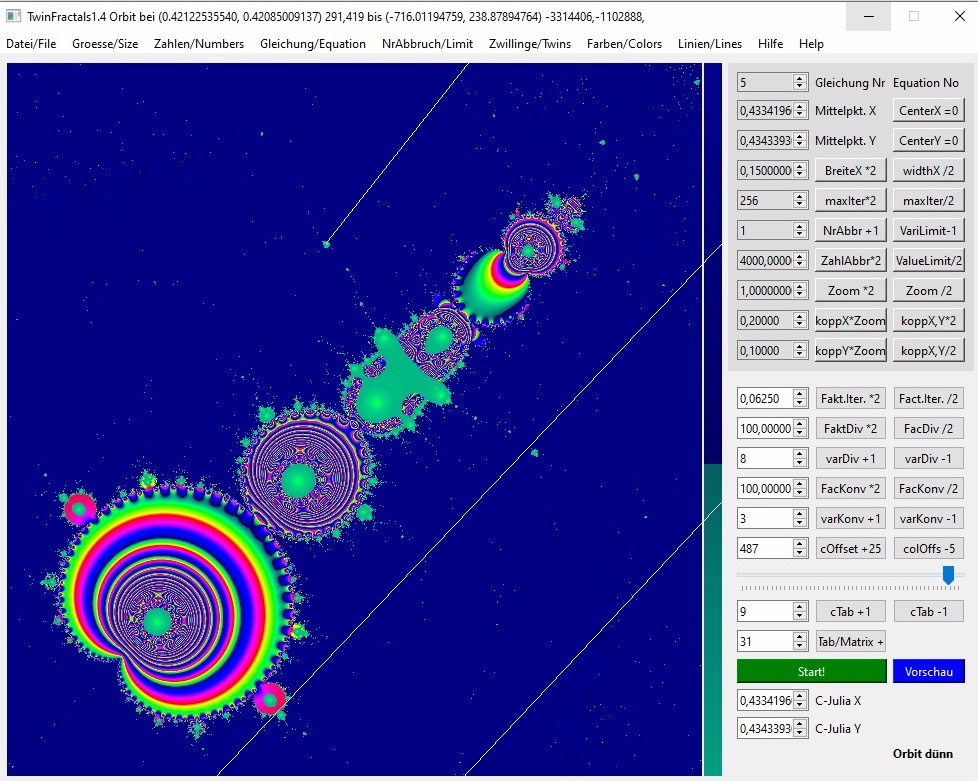
03b-11
Ein kleines Anhängsel wurde als Startpunkt angepeilt. Wieder werden die Zahlen zu groß, dass es nach Iteration 11 zum Abbruch kommt. Es dürfte sich lohnen, dort einmal hinein zu zoomen und nach Zyklen zu suchen, mit viel größeren Werten von ZahlAbbr als 4000.
1. (0.4274843482014306, 0.4724328251798579) 319,180
2. (0.9742597724734960, 1.1648353527923612) 2849,-3024
3. (-1.5583463463804859, -0.4955670009788332) -8867,4657
4. (-0.1690075450618323, -0.3192665016250246) -2439,3842
5. (0.2574660206546207, 0.1443587607077527) -467,1698
6. (0.7002113776287668, 0.6160012616015048) 1581,-485
7. (2.5844761216767855, 1.8422193807030216) 10299,-6158
8. (-0.0839344528196340, -0.1760850412599104) -2046,3179
9. (0.3439930088428704, 0.2942534018371145) -67,1004
10. (0.8282803969141629, 0.8045072864630425) 2174,-1357
11. (40.2054968297576920, 79.5076361885104319) 184359,-365503
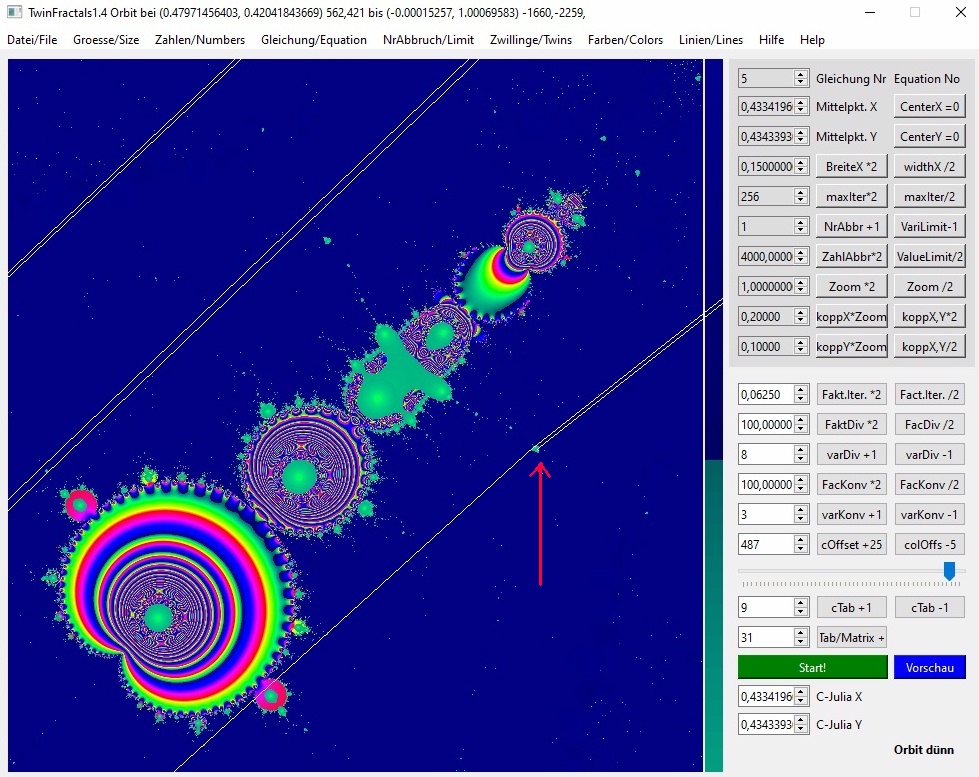
03b-12
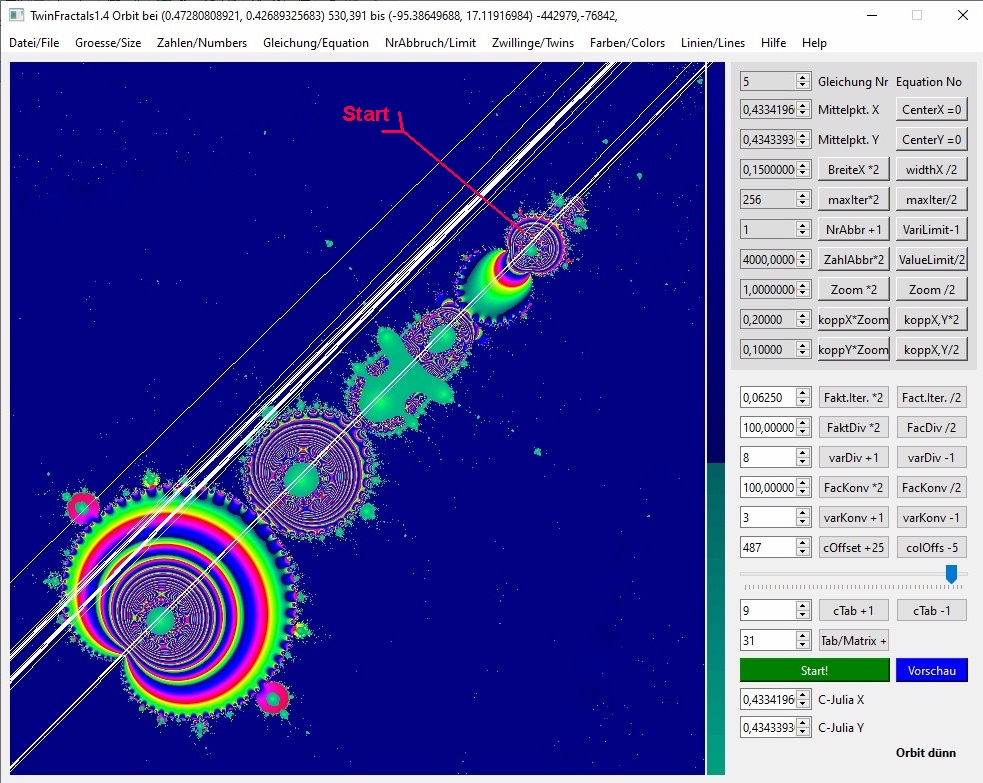
Ähnlich wie Bild 11. Zunächst sieht es nach einem 12-er Zyklus aus, aber Iteration 23 gerät außer Kontrolle, was sich schon bei Iteration 11 andeutet.
1. (0.4728080892086194, 0.4268932568345395) 529,390
2. (1.1660420237296878, 0.9715601227637671) 3736,-2130
3. (-0.4797029234644887, -1.5629137598605802) -3877,9596
4. (-0.3252698809617418, -0.1679941024375609) -3162,3142
5. (0.1384346953566234, 0.2579736034890310) -1018,1172
6. (0.6096010553405082, 0.6996093922374897) 1162,-871
7. (1.7750265558885059, 2.5465444894561102) 6554,-9417
8. (-0.1873737987852754, -0.0834758291825477) -2524,2751
9. (0.2830717390223308, 0.3440649458249669) -349,774
10. (0.7879356774725885, 0.8267509240019288) 1987,-1460
11. (13.0440617841099868, 29.5549556611856055) 58692,-134380
12. (-0.0015252873226817, -0.0001359760257508) -1665,2365
13. (0.4712828016453205, 0.4267572822431125) 522,391
14. (1.1621198787150386, 0.9718770965725306) 3718,-2131
15. (-0.4931004687397514, -1.5760894144703570) -3939,9657
16. (-0.3202862344773378, -0.1628996415950004) -3139,3118
17. (0.1436814055802513, 0.2633235950694049) -994,1147
18. (0.6150381410399016, 0.7062544375433306) 1187,-902
19. (1.8066041093319762, 2.6491726692848787) 6700,-9892
20. (-0.1751971413087736, -0.0738984471544295) -2468,2706
21. (0.2957045544667800, 0.3536591015879617) -290,729
22. (0.8063935171873374, 0.8427091373213215) 2072,-1534
23. (-95.3864968803377593, 17.1191698396358731) -442979,-76842
03b-13
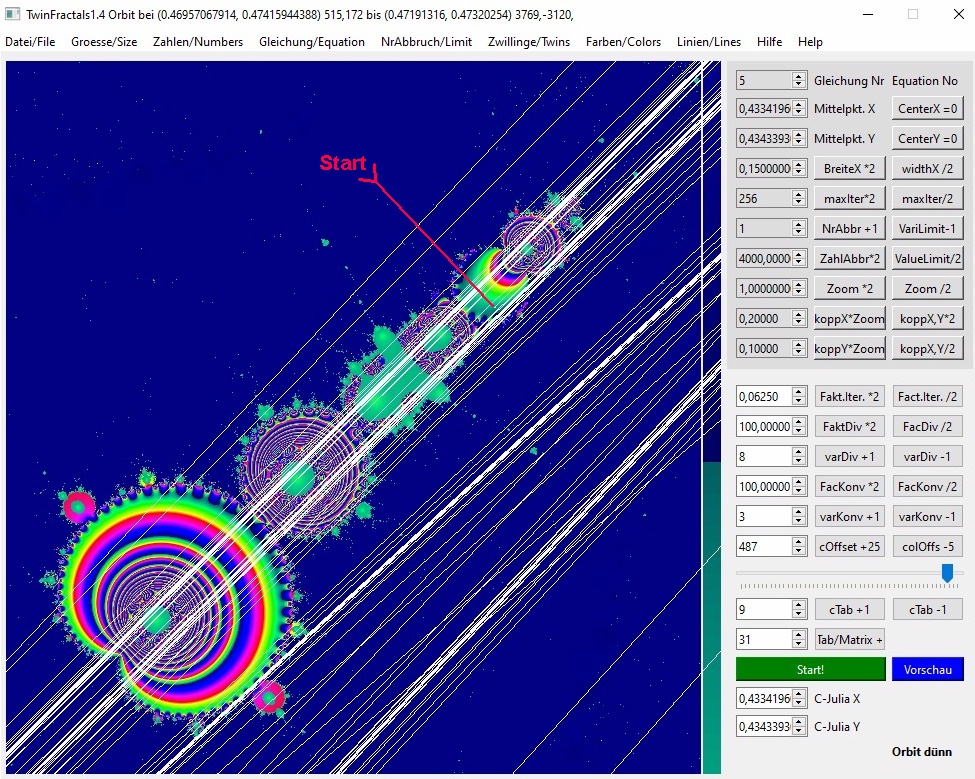
Hier ein klarer Achter-Zyklus.
235. (-0.8076745264938169, -0.7672866135251548) -5394,5915
236. (-0.1705892498992848, -0.1585517041596241) -2447,3098
237. (0.2962218463436856, 0.3132429290375776) -288,916
238. (0.8046990874502669, 0.8357255798147464) 2065,-1501
239. (-23.6123899927197698, 5.1082144729213042) -110904,-21269
240. (0.0023424863390166, -0.0009568996945757) -1648,2369
241. (0.4719131588593437, 0.4732025412863443) 525,176
242. (1.1729996536622871, 1.1855930106416919) 3769,-3120
243. (-0.8076745265008003, -0.7672866135356348) -5394,5915
244. (-0.1705892499004753, -0.1585517041621502) -2447,3098
245. (0.2962218463424474, 0.3132429290349567) -288,916
246. (0.8046990874485113, 0.8357255798107328) 2065,-1501
247. (-23.6123899952631575, 5.1082144756591434) -110904,-21269
248. (0.0023424863386026, -0.0009568996939178) -1648,2369
249. (0.4719131588589296, 0.4732025412870021) 525,176
250. (1.1729996536609786, 1.1855930106437256) 3769,-3120
03b-14
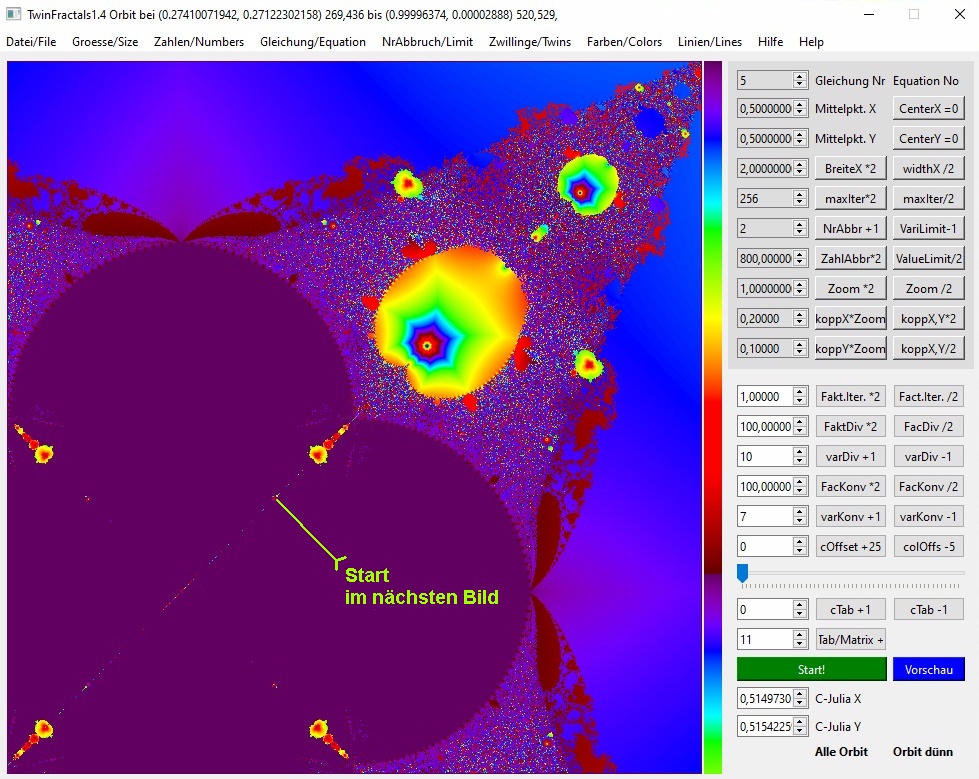
Auch ein Achter, aber deutlich weniger konvergent bis zur Iteration 250. Das eine Umkehr-Pixel (30425,-27179) von Iteration 223 schwankt noch immer in Iteration 247 (30427,-27178), während alle anderen Pixel schon in vielen Zyklen exakt nach 8 Iterationen wiederholt werden. Hier kreuzen sich auch die im Bild sichtbaren Linien. Um den ganzen Orbit zu sehen, müsste man sich so weit "entfernen", dass das hier angesteuerte Start-Pixel nicht mehr zu treffen ist. Aber eine spätere Programm-Erweiterung könnte auch das Rechnen von Orbit-Listen ganz ohne Grafik-Start ermöglichen (mit x-y-Zahlen-Einlesung).
223. (6.9344035228648586, 6.3855201541516671) 30425,-27179 <---
...
231. (6.9352301806930701, 6.3849715015686401) 30428,-27177 <---
...
235. (-1.0319795875127484, -1.1942613614076585) -6432,7890
236. (-0.1897951246666739, -0.1807058352959308) -2536,3201
237. (0.2707398924545116, 0.2745243247064341) -406,1095
238. (0.7627921709088322, 0.7615904764594411) 1871,-1158
239. (6.9345057152268161, 6.3850372306027552) 30425,-27177 <---
240. (-0.0118264844987837, -0.0142078649268560) -1712,2430
241. (0.4521313708095807, 0.4439780999881133) 433,311
242. (1.1053620783546130, 1.0741277311809976) 3456,-2604
243. (-1.0320149054239898, -1.1942664852803473) -6432,7890
244. (-0.1897924088250897, -0.1807043878970813) -2536,3201
245. (0.2707427179778290, 0.2745258252803989) -406,1095
246. (0.7627960217287523, 0.7615925323987260) 1871,-1158
247. (6.9349959345322265, 6.3852474570696724) 30427,-27178 <---
248. (-0.0118246261957824, -0.0142067536235786) -1712,2430
249. (0.4521332298042475, 0.4439792118800213) 433,311
250. (1.1053670842166072, 1.0741305386069122) 3456,-2604
03b-15
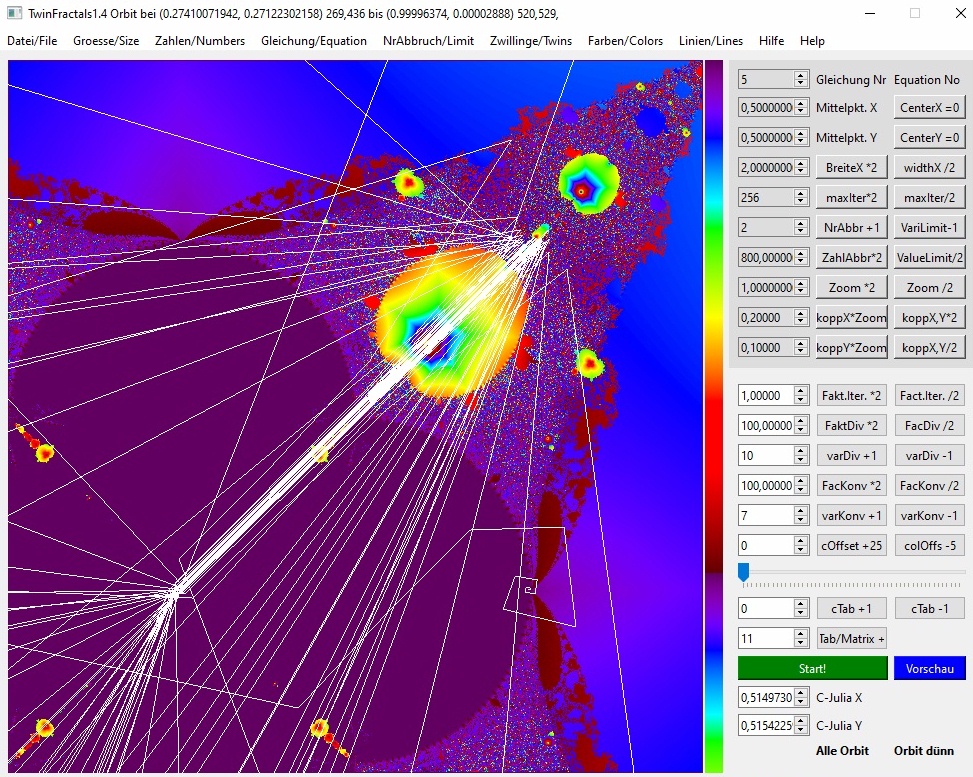
Position des Startwertes vom nächsten Bild, wo ein einziger Orbit zu sehen ist. Vermutlich sehen die meisten hier genauso aus. Es kann grafisch immer nur ein kleiner Ausschnitt betrachtet werden, weil der Startpunkt sonst im Pixel-Raster untergeht.
03b-16
Der Startpunkt ist im Bild vorher eingetragen. Offenbar habe ich das Mini-Apfelmännchen aus dieser Entfernung mit der Maus doch nicht ganz getroffen, denn es wurde am Ende kein Zyklus. Es wird Zeit, dass ich Orbit-Startpunkte mit Zahleneingabe programmiere.
Es gibt riesige Schwankungen am Anfang, die einen 10er Zyklus vermuten lassen und trotzdem läuft es am Ende in den rechten Fixpunkt bei (1,0)!
Hier der vollständige Orbit bis zum Orbit-Abbruch:
1. (0.2741007194244627, 0.2712230215827223) 269,435
2. (0.5608577766488840, 0.5544400593282672) 368,337
3. (1.0349889221282600, 1.0127609362272154) 533,178
4. (-5.3676027791029091, -8.9498644676363348) -1688,3634
5. (-0.0218188691402311, -0.0070217657372779) 167,531
6. (0.2522804686679305, 0.2642022399712035) 261,438
7. (0.5357757911533985, 0.5463177445658616) 359,340
8. (0.9739917846546263, 0.9930931767578258) 511,185
9. (-38.6442631339124318, -8.1956192054005612) -13235,3372
10. (0.0005919327599060, -0.0015382212892533) 174,529
11. (0.2746926524931708, 0.2696848008819802) 269,436
12. (0.5615381998742421, 0.5526517420008625) 368,338
13. (1.0366005246262902, 1.0082274177881951) 533,180
14. (-4.8457267926034211, -9.3760796899415944) -1507,3782
15. (-0.0220507120208851, -0.0041798186120840) 167,530
16. (0.2520491226749224, 0.2670445369988229) 261,437
17. (0.5354874661182210, 0.5495566438462318) 359,339
18. (0.9731584409431560, 1.0007037764068918) 511,182
19. (-28.7550275089141394, -3.5133059322562836) -9803,1748
20. (0.0015700720777104, -0.0026240967428868) 174,529
21. (0.2756707913812248, 0.2685989290820500) 269,436
22. (0.5626667032726980, 0.5513857404483107) 369,338
23. (1.0393464710786955, 1.0049724840323744) 534,181
24. (-4.2638944917015449, -9.4993405255030847) -1305,3825
25. (-0.0229976955872782, -0.0018333112956768) 167,529
26. (0.2511025612474898, 0.2693913915984915) 261,436
27. (0.5343810544891449, 0.5522253538282564) 359,338
28. (0.9703666180794613, 1.0069402307304167) 510,180
29. (-23.7775099009420536, -0.3732056193507006) -8076,658
30. (0.0030825335197719, -0.0033235764026817) 175,530
31. (0.2771832445620917, 0.2678994562001922) 270,437
32. (0.5644167260964499, 0.5505621576423300) 369,338
33. (1.0436739851228385, 1.0027605093203174) 536,182
34. (-3.6475070681371089, -9.3147492922870594) -1091,3761
35. (-0.0249809047502525, 0.0003753049426221) 166,529
36. (0.2491198306287579, 0.2716005426778164) 260,435
37. (0.5320863373372067, 0.5547209337308171) 358,337
38. (0.9647168096492965, 1.0126481721350300) 508,178
39. (-20.0063828845676284, 2.6287709846474243) -6768,-383
40. (0.0054197239730784, -0.0032062971003373) 175,530
41. (0.2795204061727955, 0.2680167266491889) 270,436
42. (0.5671333853636820, 0.5506760307257236) 370,338
43. (1.0505331501533783, 1.0027845109223479) 538,182
44. (-3.1110212286881027, -8.7111327443054556) -905,3551
45. (-0.0290755951294758, 0.0021021228878172) 164,529
46. (0.2450257080378421, 0.2733286021370723) 259,435
47. (0.5273851366784185, 0.5566215542328420) 357,336
48. (0.9534097232604497, 1.0165937016829172) 504,177
49. (-16.1762110950173259, 6.1898976213933210) -5439,-1618
50. (0.0085505830013842, -0.0005952524770160) 176,529
51. (0.2826512802535834, 0.2706276767090654) 272,436
52. (0.5708096048886760, 0.5536842549966902) 372,337
53. (1.0602185458890423, 1.0100486564727338) 541,179
54. (-3.0031654540870889, -7.5544188938699461) -868,3150
55. (-0.0374789188966313, -0.0000385554223918) 161,529
56. (0.2366213202528191, 0.2711917567040229) 256,435
57. (0.5178837027089783, 0.5540158598975489) 353,337
58. (0.9317379437105159, 1.0091881600328108) 497,179
59. (-10.5082207070335443, 11.2472957112636678) -3472,-3373
60. (0.0073593846779352, 0.0081164977698924) 176,527
61. (0.2814602254562327, 0.2793396797145253) 271,433
62. (0.5694777759328876, 0.5638923090844697) 371,334
63. (1.0575791736902105, 1.0366179218912210) 540,170
64. (-4.2491184129170882, -5.9458228273621687) -1300,2592
65. (-0.0407325026479993, -0.0208641341953277) 160,536
66. (0.2333556588654442, 0.2503604117856416) 254,443
67. (0.5145509303077620, 0.5305390967434380) 352,345
68. (0.9267591525714555, 0.9563800510466091) 495,198
69. (6.4082437359603386, 16.3516043367970134) 2397,-5145
70. (-0.0085706169350620, 0.0003625791196506) 172,529
71. (0.2655301136346187, 0.2715856924824399) 266,435
72. (0.5509323540913972, 0.5548600304617558) 365,337
73. (1.0102606484369814, 1.0140086561522785) 524,178
74. (-9.8385336697928878, -9.7980751590579409) -3239,3929
75. (-0.0091501267255327, -0.0093252509331670) 171,532
76. (0.2649503701487682, 0.2618975402332633) 265,439
77. (0.5502649948514753, 0.5437095860949691) 364,341
78. (1.0084187504382685, 0.9868564111639971) 523,187
79. (-6.4235774682376574, -18.4565537956306116) -2054,6933
80. (-0.0066358105908175, 0.0006731090676288) 172,529
81. (0.2674649217436925, 0.2718961723360453) 266,435
82. (0.5531675881401406, 0.5552244092423499) 365,337
83. (1.0157897663250544, 1.0149160257535546) 526,177
84. (-8.6015582913360369, -9.5351499777286328) -2810,3837
85. (-0.0117532010614739, -0.0096954321221053) 170,532
86. (0.2623470729755004, 0.2615273509706297) 265,439
87. (0.5472808277671577, 0.5432920811116579) 363,341
88. (1.0012491954190059, 0.9859714171424060) 521,187
89. (-8.7870754806423665, -21.9054877524737570) -2875,8130
90. (-0.0045850790837012, 0.0000475376835774) 173,529
91. (0.2695156408117056, 0.2712705734742170) 267,435
92. (0.5555413848380784, 0.5545029389275000) 366,337
93. (1.0216816746768560, 1.0130977501378602) 528,178
94. (-7.3881248732832283, -9.6796579632809134) -2389,3887
95. (-0.0146074555484507, -0.0085356797630813) 169,531
96. (0.2594925744542980, 0.2626873304334346) 264,438
97. (0.5440149196319419, 0.5446200794515439) 362,341
98. (0.9934900343532512, 0.9892050915180107) 518,186
99. (-15.6194980945002442, -23.2786135067308919) -5245,8606
100. (-0.0029922376337564, -0.0012816215675406) 173,529
101. (0.2711084770360347, 0.2699414018277099) 268,436
102. (0.5573843041347156, 0.5529623891983194) 367,338
103. (1.0262278448766906, 1.0092097586487374) 530,179
104. (-6.3582182050997851, -10.0651108033317751) -2032,4021
105. (-0.0165940694155914, -0.0061547995604929) 169,531
106. (0.2575059552026524, 0.2650685980668164) 263,438
107. (0.5417360058055685, 0.5473379957279996) 361,340
108. (0.9880561459964439, 0.9956684121429281) 516,184
109. (-21.4503225920177094, -17.5013862365462352) -7269,6602
110. (-0.0018268544310407, -0.0027917919325620) 174,529
111. (0.2722738640136497, 0.2684312242629224) 268,436
112. (0.5587287430983050, 0.5512102158738833) 367,338
113. (1.0294953438930112, 1.0047867461427327) 531,181
114. (-5.4622863928381316, -10.4613034120703823) -1721,4159
115. (-0.0176865272262336, -0.0034711974199274) 168,530
116. (0.2564137211218898, 0.2677525160706494) 262,437
117. (0.5404703543269336, 0.5504031166830159) 361,339
118. (0.9849556376998960, 1.0029485001736149) 515,181
119. (-21.3739545860748485, -10.9129101708285940) -7242,4315
120. (-0.0007000196868300, -0.0043777725217442) 174,530
121. (0.2734007110453287, 0.2668452429845852) 268,437
122. (0.5600245722152594, 0.5493685989385088) 368,339
123. (1.0326031051675399, 1.0001277059693998) 532,182
124. (-4.5290563554600318, -10.7515257194899423) -1397,4259
125. (-0.0184514300317214, -0.0005864390930898) 168,529
126. (0.2556491826056603, 0.2706374793394218) 262,436
127. (0.5395695097402851, 0.5537017947763655) 361,337
128. (0.9826394549706607, 1.0108087160430463) 514,179
129. (-19.0735629044616246, -6.5044758623842496) -6444,2786
130. (0.0007796995527404, -0.0062270186510869) 174,531
131. (0.2748804531588526, 0.2649960154131154) 269,438
132. (0.5617225070473556, 0.5472176778912309) 368,340
133. (1.0366455117067506, 0.9946511658129862) 533,184
134. (-3.3897908812364386, -10.8403981812232839) -1002,4290
135. (-0.0192613550674345, 0.0030261495755305) 168,528
136. (0.2548398163620598, 0.2742501410356029) 262,434
137. (0.5385984699190772, 0.5578374141308557) 360,336
138. (0.9800032069125215, 1.0207011214282262) 514,175
139. (-16.1109127049290777, -3.4290961287223913) -5416,1718
140. (0.0032818449121198, -0.0087780037583306) 175,532
141. (0.2773826256439530, 0.2624451223647254) 270,438
142. (0.5645889249886253, 0.5442396973413395) 369,341
143. (1.0434365050564938, 0.9869634706547634) 536,187
144. (-1.8603493985815323, -10.4823275737560042) -471,4166
145. (-0.0204214559605676, 0.0087598696135493) 167,526
146. (0.2536807363310713, 0.2799835123893876) 262,432
147. (0.5371729205493806, 0.5644113934557666) 360,334
148. (0.9758416426568056, 1.0365097681173909) 512,170
149. (-12.5163149205601076, -1.1397624876307753) -4169,924
150. (0.0088979284821873, -0.0133489292129330) 177,533
151. (0.2829985620571274, 0.2578746958638709) 272,440
152. (0.5710076082834153, 0.5388581176994477) 372,343
153. (1.0585136152405179, 0.9726482817366254) 541,192
154. (0.1690806896149641, -8.9892464198962507) 232,3648
155. (-0.0221286277809911, 0.0220383264817728) 167,522
156. (0.2519755388346290, 0.2932583912739249) 261,428
157. (0.5348686109039921, 0.5797047321008484) 359,328
158. (0.9674307221734549, 1.0738438996133930) 509,157
159. (-7.9101157224641394, 0.2655123725010103) -2570,437
160. (0.0293368349261677, -0.0274913818860297) 184,538
161. (0.3034307727598656, 0.2437386495760610) 279,445
162. (0.5941627767121879, 0.5217857255791766) 380,348
163. (1.1107526747024665, 0.9236294961176605) 559,209
164. (1.8965014374059090, -4.9940951125291067) 832,2262
165. (-0.0114390313862221, 0.0891482924056896) 171,499
166. (0.2625541981106693, 0.3603078639636410) 265,404
167. (0.5432257972327916, 0.6599894253077290) 362,300
168. (0.9490219073599668, 1.2947144109870004) 503,80
169. (-2.4020896868896338, 0.2584579566183920) -659,440
170. (0.3349705539292513, -0.3446888697792166) 290,648
171. (0.6123598258241457, -0.0473750400476060) 386,545
172. (0.8311126636526999, 0.1720186561824282) 462,470
173. (1.1009772979770367, 0.1802650045204592) 556,467
174. (1.1362462805626361, -0.1112315452330969) 568,567
175. (0.9253661187921652, -0.0588424746509717) 495,549
176. (0.9605920432435111, 0.0383796112096743) 507,516
177. (1.0242267894094990, 0.0286413150164600) 529,520
178. (1.0186097799327900, -0.0168898444348641) 527,534
179. (0.9892058058412982, -0.0113017006300782) 517,532
180. (0.9927533077229382, 0.0066071150055702) 518,527
181. (1.0041895968658214, 0.0047571546073091) 522,528
182. (1.0030608843176763, -0.0027047829575126) 522,529
183. (0.9982788556760355, -0.0019486178729524) 520,529
184. (0.9987492854639201, 0.0010867536561435) 520,529
185. (1.0006901730926587, 0.0008061681021364) 521,529
186. (1.0005179276504146, -0.0004397138425915) 521,529
187. (0.9997205386625929, -0.0003321329104277) 520,529
188. (0.9997867470378315, 0.0001773553367342) 520,529
189. (1.0001126564957221, 0.0001370187297592) 521,529
190. (1.0000879877326607, -0.0000715965694276) 521,529
191. (0.9999545192177655, -0.0000564820562126) 520,529
192. (0.9999637366932813, 0.0000288818802841) 520,529
03b-17
Hier habe ich den Startpunkt von Bild 16 zum Mittelpunkt (0.2741007194244627, 0.2712230215827223) gemacht und habe die Bildbreite extrem verkleinert.
03b-18
Und jetzt nochmal näher heran gegangen, immer mit denselben Farbeinstellungen bei maxIter=256.
Eindeutig: Knapp daneben ist auch vorbei. Fast wie beim Attentat auf Trumps Ohr. Nur gelingt hier der genaue Nachweis.
03b-19
Jetzt wurde maxIter=5000 gesetzt, aber es musste die Farbeinstellung geändert werden.
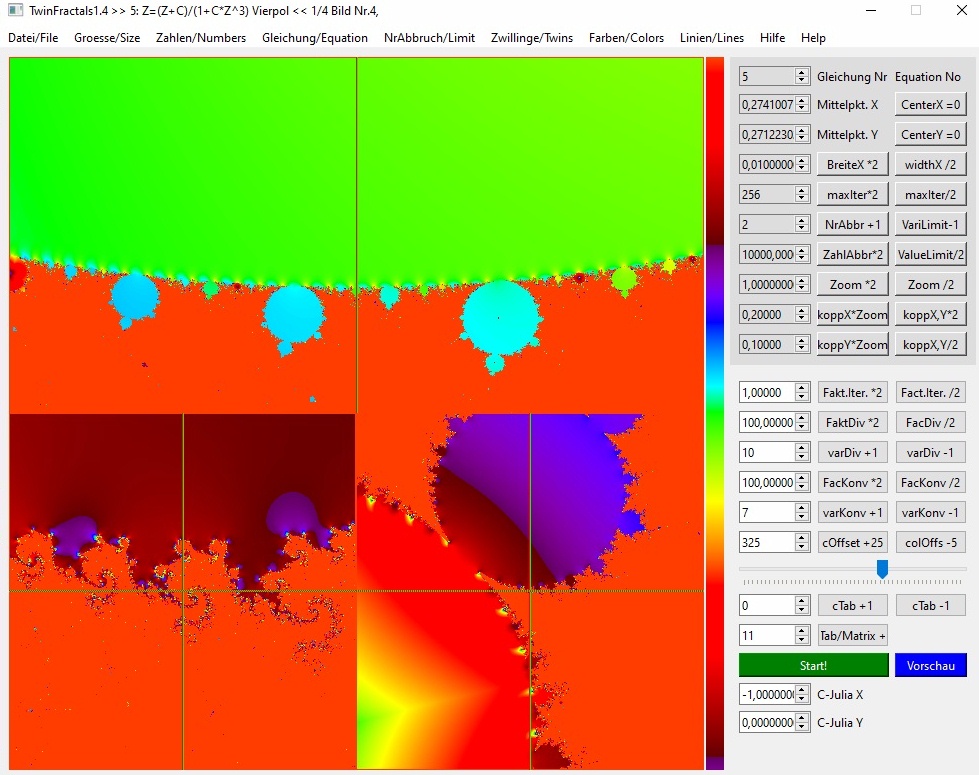
03b-19-kombi
Bild 18 und 19 zusammen gezeigt. Mit der neuen Farbeinstellung wurden als Viertelbilder 3 und 4 die Bilder aus größerer Entfernung (gleicher Mittelpunkt), aber wieder mit maxIter=256 noch einmal dazu gerechnet, zum direkten Vergleich.
Ergebnis: Die ganzen Spiralen im Apfelmännchen sind immer nur virtuelle Gebilde, die nur dann auftreten, wenn die Iterationen zu früh abgebrochen werden. Hier im Vierpol ist der Außenbereich aber keine Flucht nach Unendlich. Stattdessen wird einer der vier Fixpunkte gefunden. Aber je näher an der Diagonale und einer solchen Pseudo-Null, desto länger gibt es eine Lebenszeit/Einschwingzeit, ein taumelndes Herumtappen im Umfeld, ein Suchen nach dem "Heimweg", als ob ein Magnetfeld zu dem Fixpunkt führt. Von innerhalb der "Kaktus-Null" gibt es kein Entkommen, die Zyklen wiederholen sich ewig, wie das Kreisen in einem Schwarzen Loch.
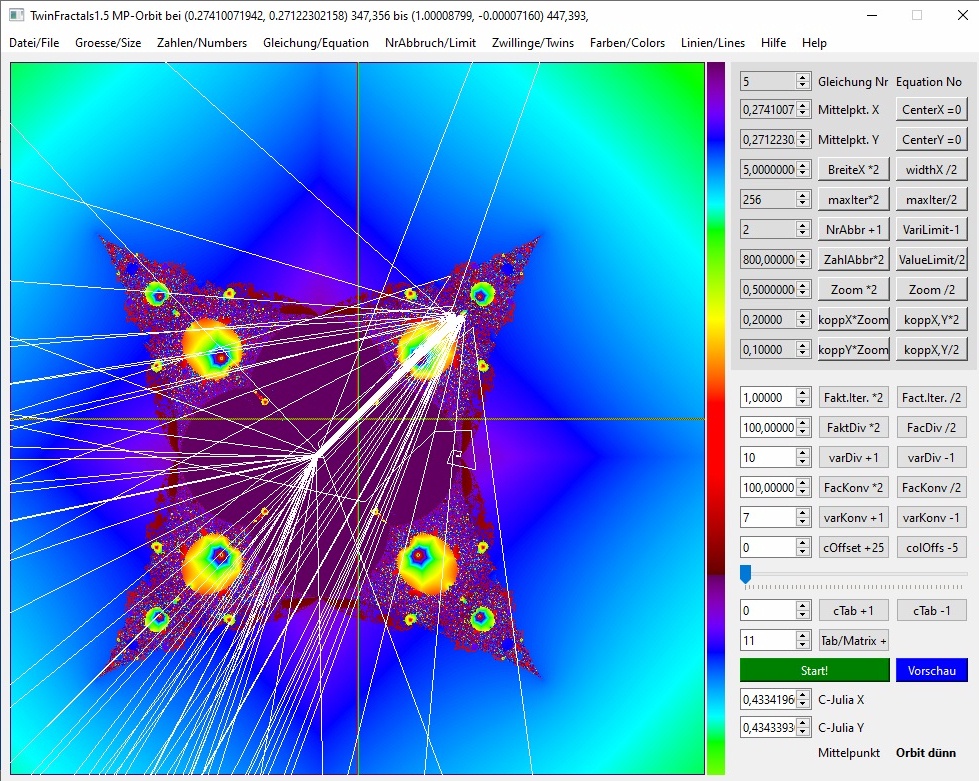
03b-19a
Bild 16 mit Orbit-Startpunkt im Bildzentrum. Version 1.5 ist in Vorbereitung. Der Orbit lässt sich jetzt aus dem Bildmittelpunkt heraus berechnen. Der kann in der Nahaufnahme angepeilt/eingestellt werden, und trotzdem kann das vergrößerte Bild denselben Orbit im Ganzen grafisch darstellen, wenn der alte Mittelpunkt erhalten bleibt. Dazu gibt es eine neue Einstellung im Menü Linien bei Orbits.
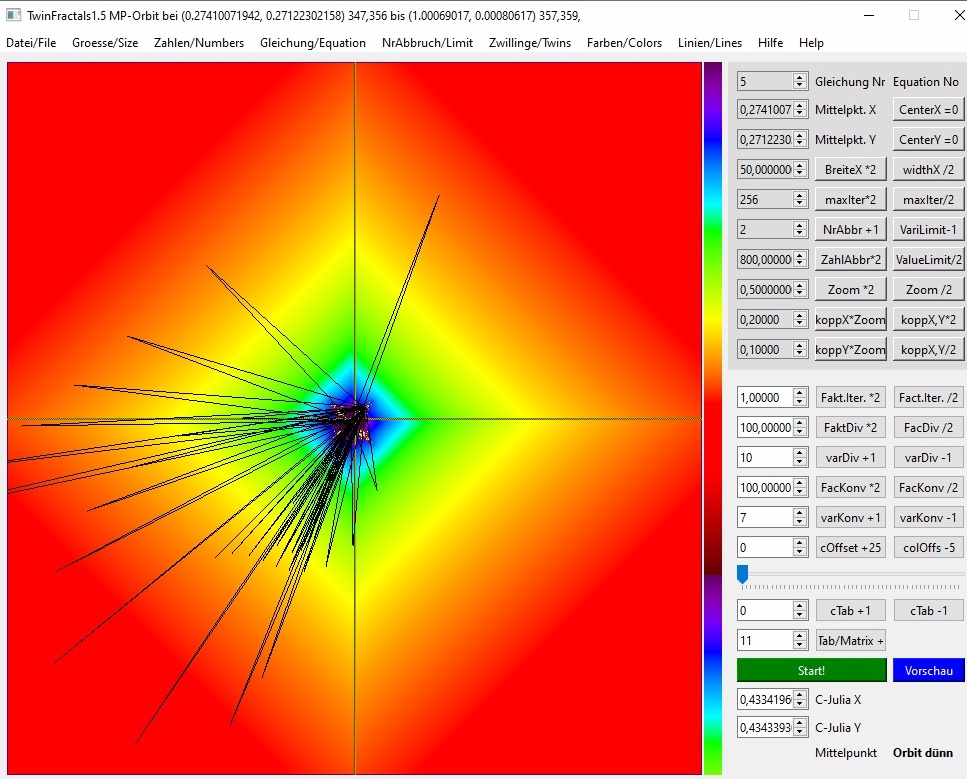
03b-19b
Wie Bild 19a, aber Bildbreite 50.0 neue Orbit-Liste . Die Liste ist etwas kürzer als am Vortag, weil das Übertragen der Orbit-Start-Zahlen doch eine kleine Verkürzung erfuhr beim Eintragen per Kopie in die beiden Mittelpunkt-Textfelder. Aber zahlenmäßig ist alles fast gleich.
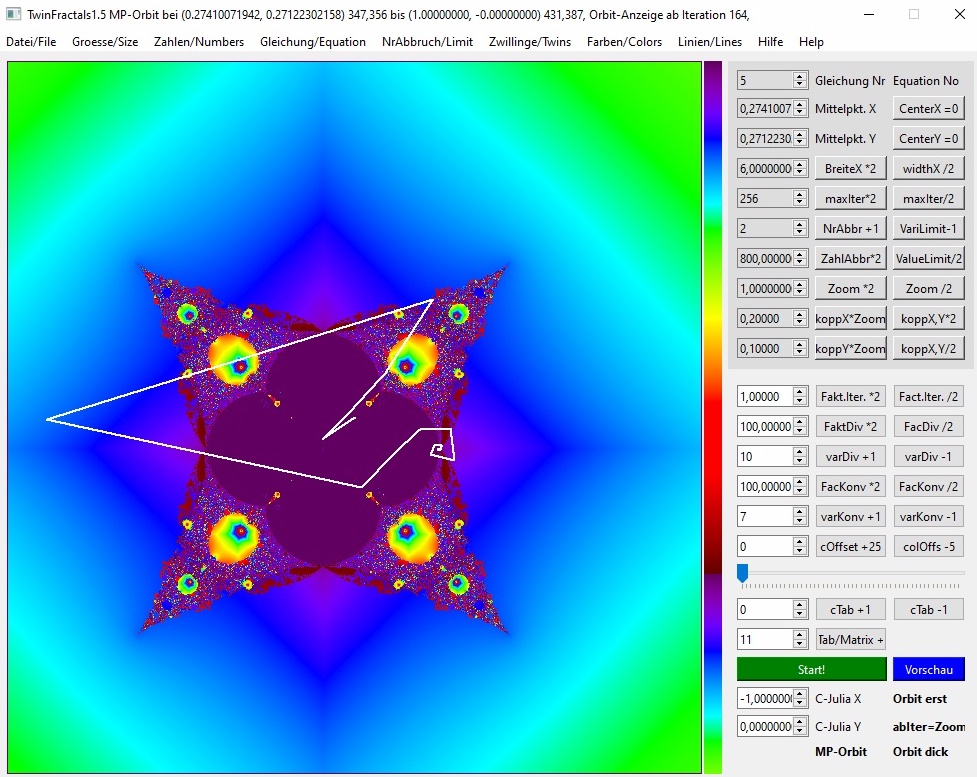
03b-19c
Auch NEU in Version1.5: Wie Bild 19a, aber alle Iterationen bis zur 164. wurden nicht angezeigt und stehen auch nicht in der Orbit-Liste. So kann man das überschwingende Einschwingen ausblenden. Bei Zyklen lässt sich der wiederholende Ergebnis-Zyklus einzeln sauber anzeigen, wenn man die richtige OrbitStart-Iteration vor dem Schluss der Liste auswählt. Auf diese Weise können die maxIterat auch viel höher liegen - Ab der bei Linien/( Orbit erst ab Iterat EIN) eingetragenen Zahl (vorher bei ZOOM eingestellt/+Start!) werden 256 Werte gezeichnet und gelistet, nach Auswahl von Datei/(Letzten Orbit als Liste in HTML-Seite speichern).
Oder auch weniger, wenn auch Linien/(maximal x Iterationen) ausgewählt wurde.
Wenn ich es wage, über Aggregatzustände (AGZ) zu fabulieren, ist Bild 19c eher Gas, Flüssigkeit und Festkörper (Fixpunkt), als möglicher Zustand der Punkt-Dynamik, während Bild 19b auch verschiedene höhere AGZ anzeigt: Plasma, E-Feld, H-Feld (weit außen). Die Mitte (Bild 19c) ist der beruhigte Zustand, das Kondensat, also kälter, langsamer und später.
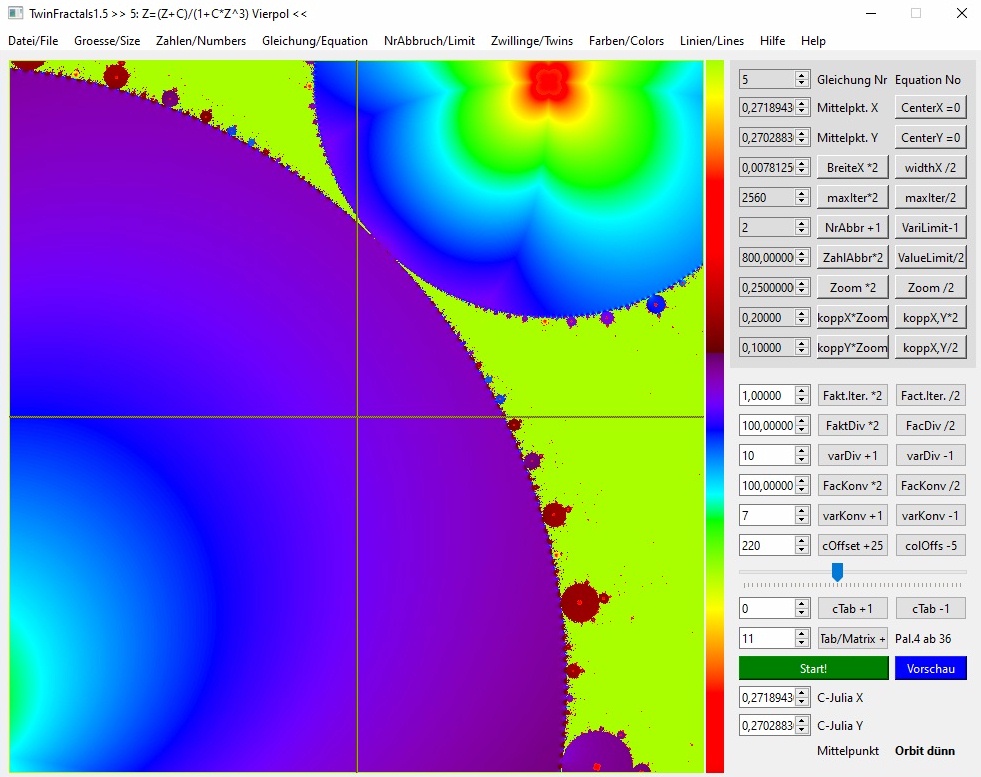
03b-20
Hier wieder das Motiv in der Nähe von Bild 17 bis 19c, aber diesmal ist der Startpunkt drin im Hauptkörper.
03b-21
Hier konnte schon die Orbit-Liste gespeichert werden. Der Startpunkt ist am Schnittpunkt vom Mittelkreuz. Bis hierhin hätte man auch mit Version 1.4 arbeiten können.
Fünfer-Zyklus, letzte Punkte:
239. (-12.4790090638552336, -16.5261793753802806) -1132340,1492473
240. (-0.0051983690001486, -0.0029341852563005) -24266,24627
241. (0.2666959075411003, 0.2673541167555121) -114,617
242. (0.5499358094768858, 0.5489850673193352) 25046,-24402
243. (1.0033002436466352, 0.9977435049857941) 65320,-64267
244. (-12.4700658434384870, -16.5206613267641451) -1131545,1491983
245. (-0.0052043104396887, -0.0029350464007341) -24267,24627
246. (0.2666899660163297, 0.2673532556470924) -115,617
247. (0.5499289693672645, 0.5489840769339868) 25046,-24402
248. (1.0032836962892162, 0.9977411920529542) 65318,-64267
249. (-12.4782883005556933, -16.5242682950287367) -1132276,1492304
250. (-0.0051991801992376, -0.0029350231096888) -24266,24627
03b-22
Es war Bildbreite 50.0 nötig, um einen Überblick über die wahre Größe des Orbits zu erhalten, und 50 reicht nichtmal. Der Start wieder exakt am alten MP-Wert, ohne Beachtung der vergrößerten Schrittweite zwischen den Pixeln, die zu einem neuen Mittelpunkt-Pixel führen würde. Die MPxy-Zahlen können seit Version 1.5 (optional) direkt als Orbit-Start eingetragen werden.
htm-Datei Orbit-Liste
Letzte Punkte identisch wie in Bild 21, nur sinnvolle Pixelgrößen:
239. (-12.4790090638552336, -16.5261793753802806) 171,588
240. (-0.0051983690001486, -0.0029341852563005) 344,359
241. (0.2666959075411003, 0.2673541167555121) 347,356
242. (0.5499358094768858, 0.5489850673193352) 351,352
243. (1.0033002436466352, 0.9977435049857941) 357,346
244. (-12.4700658434384870, -16.5206613267641451) 171,588
245. (-0.0052043104396887, -0.0029350464007341) 344,359
246. (0.2666899660163297, 0.2673532556470924) 347,356
247. (0.5499289693672645, 0.5489840769339868) 351,352
248. (1.0032836962892162, 0.9977411920529542) 357,346
249. (-12.4782883005556933, -16.5242682950287367) 171,588
250. (-0.0051991801992376, -0.0029350231096888) 344,359
03b-23
Das Gleiche im Kopf.
03b-24
Orbit beginnt am Bildmittelpunkt/Kreuz. Orbit-Liste
Ein Zehner-Zyklus am Ende, der bei 250 noch nicht gut eingeschwungen war. Ich muss noch optional den Orbit-Endpunkt auf über 250 erhöhen. Demnächst.
239. (-41.9781910627215069, 9.8770130365201947) -3753008,-852901
240. (0.0013122848934308, -0.0004452680601848) -23886,24564
241. (0.2754242611896785, 0.2716215253335629) 464,396
242. (0.5624109011897449, 0.5558004002984250) 25958,-24849
243. (1.0390329715267215, 1.0179103564932748) 68297,-65901
244. (-5.2396270339991124, -8.0130773682838807) -489448,736368
245. (-0.0250670959906588, -0.0102162432232309) -26228,25432
246. (0.2490423187254036, 0.2618515988795188) -1880,1264
247. (0.5321191549830899, 0.5445094300099809) 23267,-23846
248. (0.9655179530277778, 0.9903523761050672) 61766,-63453
249. (-41.9644675252433927, 9.8723633741295505) -3751789,-852488
250. (0.0013131311451007, -0.0004456526920455) -23886,24564
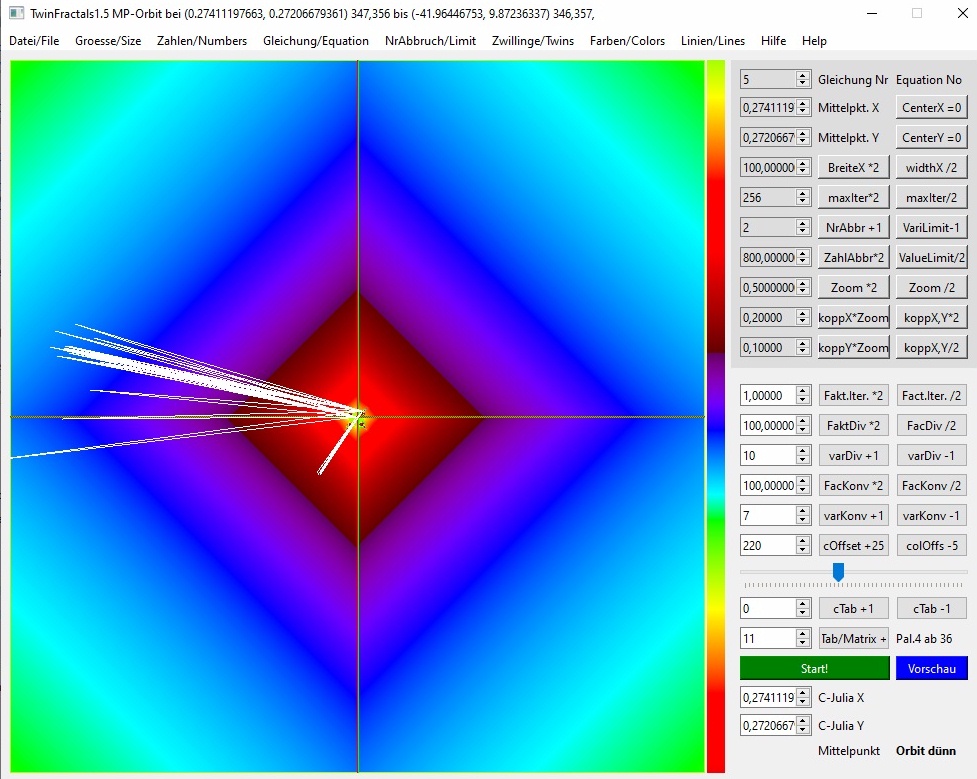
03b-25
Diesmal war Bildbreite 100.0 nötig. Da sowieso der Orbit bei 250 abgebrochen wird, habe ich beim Bildrechnen gleich das maxIter=256 gesetzt (Einzelheiten hier nicht sichtbar, geht viel schneller, hat aber Einfluss auf die Farben).
Orbit-Liste
weiter
1 Seite zurück
zurück zu Fraktale